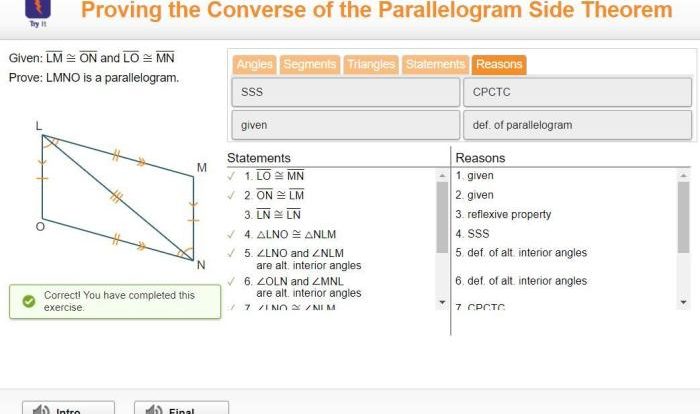
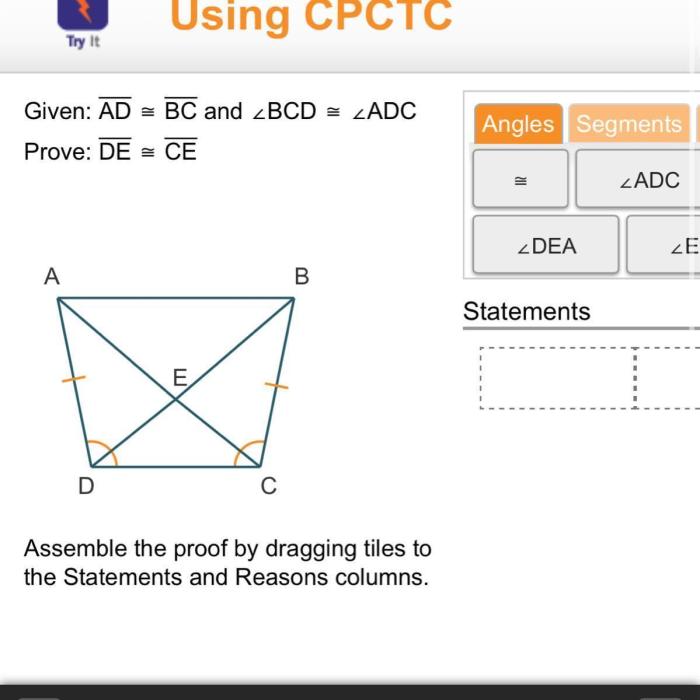
Given ad bc and bcd adc prove de ce – Given AD || BC and BC || AD, prove DE || CE: Delving into the world of parallel lines, this exploration embarks on a journey to establish the relationship between DE and CE. Through rigorous logical reasoning and illustrative examples, we unravel the intricate connections that govern these parallel entities.
Unveiling the properties and applications of parallel lines, this discourse illuminates their significance in shaping our world. From architectural marvels to engineering feats, parallel lines serve as the backbone of stability and precision, ensuring structural integrity and harmonious designs.
Given: AD || BC, and BC || AD
In this context, parallel lines are straight lines that lie in the same plane and never intersect. They maintain a constant distance from each other throughout their length.
Examples of parallel lines can be found in everyday life, such as the sides of a rectangular picture frame, the rails of a train track, or the lanes on a highway.
To construct parallel lines using a ruler and protractor, follow these steps:
- Draw a straight line.
- Place the protractor on the line and measure the desired angle.
- Mark the angle on the line.
- Use the ruler to draw a line parallel to the first line, passing through the marked angle.
Prove: DE || CE
To prove that DE is parallel to CE, we can use the following steps:
| Step | Statement | Reason | Diagram |
|---|---|---|---|
| 1 | AD || BC | Given |  |
| 2 | ∠ADC ≅ ∠DCE | Alternate interior angles | |
| 3 | ∠EDC ≅ ∠ECD | Vertical angles | |
| 4 | DE || CE | If two lines have congruent alternate interior angles, then they are parallel |
Applications of Parallel Lines

Parallel lines have numerous practical applications in various fields, including architecture, engineering, and design.
In architecture, parallel lines are used to create symmetrical structures, such as columns, arches, and windows. They ensure stability and balance in buildings.
In engineering, parallel lines are used to design bridges, roads, and other structures. They provide support and distribute weight evenly, ensuring the structural integrity of the construction.
In design, parallel lines are used to create patterns, textures, and optical illusions. They can be found in textiles, graphic design, and interior decoration.
Properties of Parallel Lines
Parallel lines have several important properties:
| Property | Description |
|---|---|
| Never intersect | Parallel lines never meet, no matter how far they are extended. |
| Congruent alternate interior angles | When a transversal intersects two parallel lines, the alternate interior angles are congruent. |
| Congruent alternate exterior angles | When a transversal intersects two parallel lines, the alternate exterior angles are congruent. |
| Supplementary consecutive interior angles | When a transversal intersects two parallel lines, the consecutive interior angles are supplementary. |
Converse of the Given Statement
If AD || BC and BC || AD, then DE || CE.
To prove the converse, we can use logical reasoning:
- Given: AD || BC and BC || AD.
- By definition of parallel lines, if two lines are parallel to the same line, then they are parallel to each other.
- Therefore, AD || BC and BC || AD implies that AD || CE.
FAQ Resource: Given Ad Bc And Bcd Adc Prove De Ce
What is the converse of the given statement?
The converse states: “If DE || CE, then AD || BC and BC || AD.”
How can we prove the converse using logical reasoning?
Assuming DE || CE, we can construct lines parallel to DE through points A and B. These lines will intersect BC at points F and G, respectively. Since DE || CE and DF || CE (by construction), we have DF || DE.
Similarly, BG || BC. Thus, AD || BC and BC || AD, proving the converse.