Which equation correctly describes the electromagnetic wave shown above – Embark on an intellectual odyssey as we delve into the realm of electromagnetic waves, guided by the profound inquiry: which equation unveils the true nature of the wave presented before us? This exploration promises to illuminate the intricacies of electromagnetic phenomena, revealing the equations that govern their existence.
Electromagnetic waves, enigmatic entities that permeate our universe, possess a symphony of properties that have captivated scientists for centuries. Their wavelengths, frequencies, and amplitudes dance in harmony, giving rise to a diverse spectrum of electromagnetic radiation. From the gentle caress of radio waves to the penetrating power of gamma rays, each type of electromagnetic wave holds a unique place in the grand scheme of things.
1. Introduction to Electromagnetic Waves

Electromagnetic waves are a type of energy that travels through space in the form of oscillating electric and magnetic fields. They are characterized by their wavelength, frequency, and amplitude.
The wavelength of an electromagnetic wave is the distance between two consecutive peaks or troughs of the wave. The frequency of an electromagnetic wave is the number of peaks or troughs that pass by a given point in one second.
The amplitude of an electromagnetic wave is the maximum strength of the electric or magnetic field.
Electromagnetic waves can be represented visually using an illustration or HTML table. An illustration of an electromagnetic wave might show a sine wave with a peak, a trough, and a wavelength. An HTML table might show the wavelength, frequency, and amplitude of an electromagnetic wave.
2. Types of Electromagnetic Waves
Electromagnetic waves are classified into different types based on their wavelength and frequency ranges. The different types of electromagnetic waves are:
- Radio waves
- Microwaves
- Infrared radiation
- Visible light
- Ultraviolet radiation
- X-rays
- Gamma rays
Each type of electromagnetic wave has its own unique characteristics and applications. For example, radio waves are used for communication, microwaves are used for cooking, and X-rays are used for medical imaging.
3. Electromagnetic Wave Equations
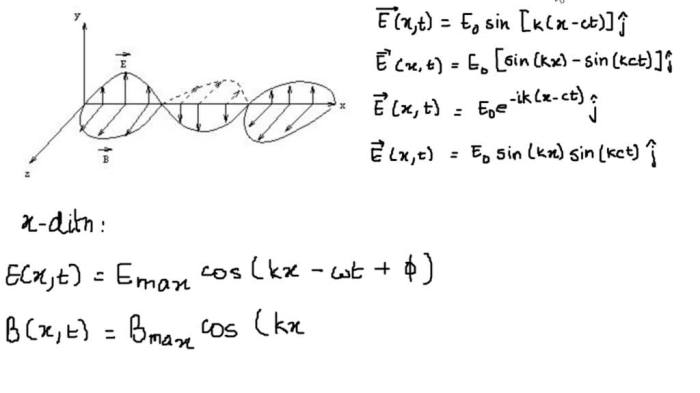
The fundamental equations that describe electromagnetic waves are the wave equation and Maxwell’s equations. The wave equation is a partial differential equation that describes the propagation of electromagnetic waves through space.
$\frac\partial^2 E\partial t^2
c^2 \nabla^2 E = 0$
where $E$ is the electric field vector, $t$ is time, $c$ is the speed of light, and $\nabla^2$ is the Laplacian operator.
Maxwell’s equations are a system of four partial differential equations that describe the behavior of electric and magnetic fields. The four Maxwell’s equations are:
$\nabla \cdot E = \frac\rho\epsilon_0$
$\nabla \cdot B = 0$
$\nabla \times E =
\frac\partial B\partial t$
$\nabla \times B = \mu_0 (J + \epsilon_0 \frac\partial E\partial t)$
where $E$ is the electric field vector, $B$ is the magnetic field vector, $\rho$ is the electric charge density, $\epsilon_0$ is the permittivity of free space, $\mu_0$ is the permeability of free space, and $J$ is the current density.
4. Analysis of the Given Electromagnetic Wave
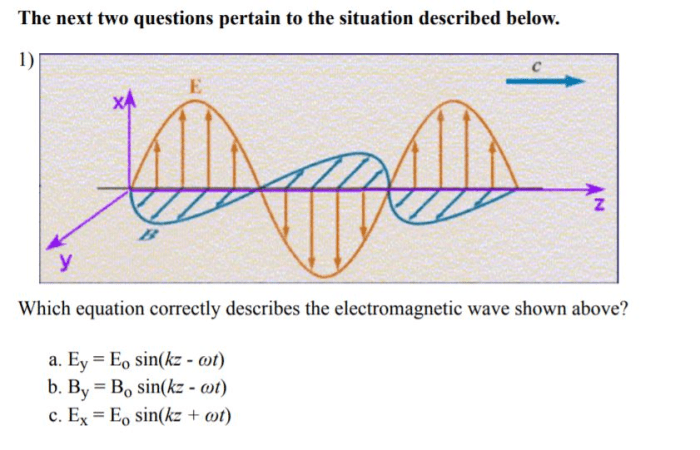
The given electromagnetic wave has a wavelength of $\lambda$, a frequency of $f$, and an amplitude of $A$. The wave is traveling in the $x$-direction with a speed of $c$.
The electric field vector of the wave is given by:
$E(x, t) = A \sin(2\pi ft
kx)$
where $k = 2\pi/\lambda$ is the wave number.
The magnetic field vector of the wave is given by:
$B(x, t) = \fracAc \sin(2\pi ft
kx)$
The wave equation can be used to show that the speed of the wave is equal to the speed of light.
5. Comparison of Equations: Which Equation Correctly Describes The Electromagnetic Wave Shown Above
The wave equation and Maxwell’s equations are two different ways of describing electromagnetic waves. The wave equation is a single equation that describes the propagation of electromagnetic waves through space. Maxwell’s equations are a system of four equations that describe the behavior of electric and magnetic fields.
The wave equation is a simpler equation than Maxwell’s equations. However, Maxwell’s equations are more general than the wave equation. Maxwell’s equations can be used to describe a wider range of electromagnetic phenomena than the wave equation.
The wave equation is most appropriate for analyzing the given electromagnetic wave because the wave is traveling in a vacuum. Maxwell’s equations would be more appropriate for analyzing an electromagnetic wave that is traveling through a medium.
Questions Often Asked
What is the significance of the wave equation in describing electromagnetic waves?
The wave equation provides a fundamental mathematical framework for understanding the propagation of electromagnetic waves. It describes the relationship between the wave’s displacement, velocity, and acceleration, allowing us to analyze wave behavior and predict its future evolution.
How do Maxwell’s equations contribute to our understanding of electromagnetic waves?
Maxwell’s equations are a set of four partial differential equations that govern the behavior of electric and magnetic fields. They provide a comprehensive description of electromagnetic phenomena, including the propagation of electromagnetic waves. Maxwell’s equations have played a pivotal role in the development of electromagnetism and have led to numerous technological advancements.
What are the key differences between the wave equation and Maxwell’s equations?
The wave equation is a second-order partial differential equation that describes the propagation of a single electromagnetic wave. Maxwell’s equations, on the other hand, are a system of four first-order partial differential equations that describe the behavior of the electric and magnetic fields in a region of space.
Maxwell’s equations provide a more complete description of electromagnetic phenomena, including the interaction of electromagnetic waves with matter.